|
|
||
|---|---|---|
| examples | ||
| rsrc | ||
| src | ||
| .gitignore | ||
| README.md | ||
README.md
(CAM) Fifth
The following is a Cellular Automata Machine (CAM) library loosely based off the CAM Forth language as described in "Cellular Automata Machines" by Toffoli and Margolus. I wanted to be able to follow along in the book but, though mentioned as reasonably priced, a CAM Forth machine is out of my price range.
The following uses numpy/matplotlib underneath, and will ideally incorporate the following:
- N-Dimensional Cellular Automata
- Arbitrary count of bit planes and description of neighborhoods
- Timing specifications and control for granular viewing
- ECHOing and TRACing in library for 2D CAMs
Documentation will be made available at fuzzykayak.com/... but a quickstart will be provided below. There are also a variety of examples given to demonstrate different means of building CAMS.
Quickstart
To begin construction of a CAM, we need two objects: a CAM and a Ruleset.
A CAM can be broken down into a list of cell planes, each of which contain the same number of states. Of these planes, the first is considered the master, and all others are mirrors of the master at an earlier stage in time (this allows for methods such as ECHOing).
A ruleset can further be broken down into a list of configurations, of which one must pass for the state of a cell to change. During application of a ruleset, each cell is described by a neighborhood, which packages all other cells considered in the given plane.
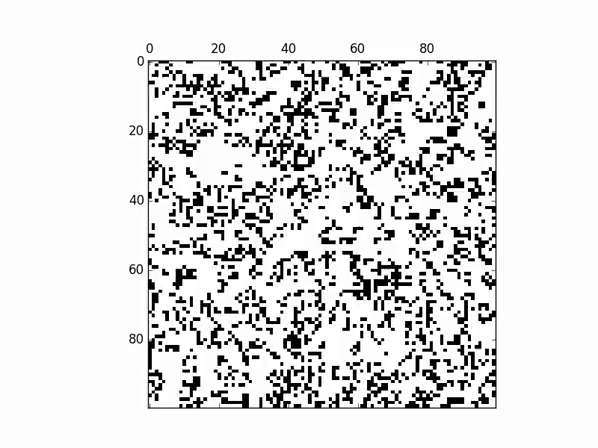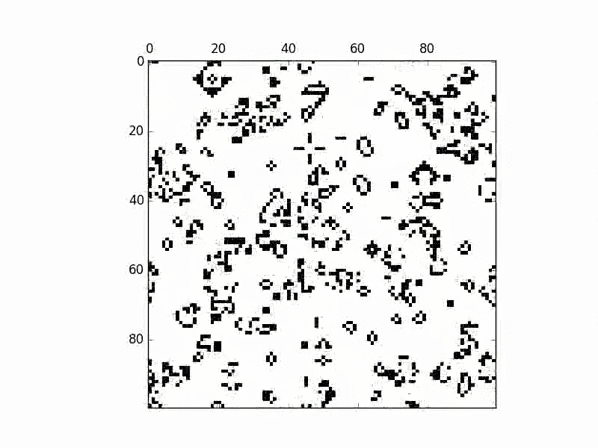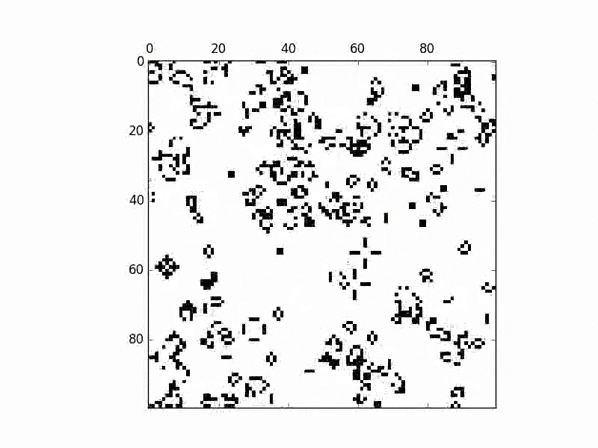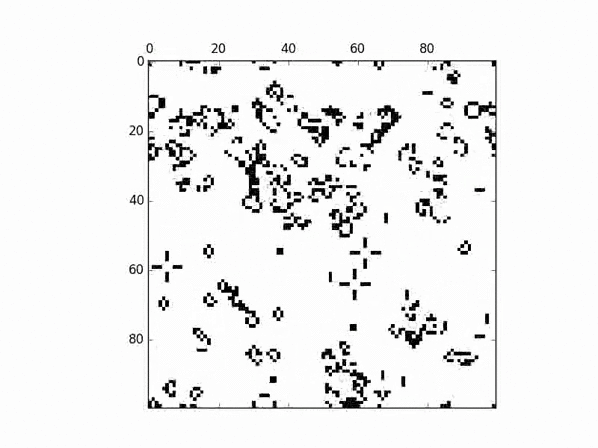
The following will construct Conway's Game of Life, as shown in the provided GIF:
import cam
import ruleset as rs
# View the different formats the CAMParser can parse. Manual construction for
# more complicated rulesets are also a possibility
c = cam.CAM(1, 100, 2)
p = u.CAMParser('B3/S23', c)
# 400 represents the time, in milliseconds, before the next tick occurs
c.randomize()
c.start_plot(400, p.ruleset)